02. Information Theory
2.1 Entropy
\[S(x) = -\log_2 p_X(x)\]놀람도 (Surprisal)
어떤 사건이 발생했을 때 느끼는 놀라움의 정도.
- 사건이 드물수록 $p_X(x)$ 값이 작아져 놀람도가 커진다.
- 단위는 bits (밑이 2인 로그 사용).
Example 2
$X$: 지진 발생 여부를 나타내는 indicator
- $X = 1$: 큰 지진 발생
- $X = 0$: 지진 아님
만약 $p_X(1)$이 매우 작다면, $X=1$은 매우 놀라운 사건이다.
\[H(X) = E[-\log_2 p_X(X)] = \sum_{x \in X} p_X(x) \log_2 \frac{1}{p_X(x)}\]엔트로피 (Entropy)
확률변수 $X$의 평균 놀람도 (기댓값)
Example 4
Binary random variable, $p(1) = 0.01$, $p(0) = 0.99$
Example 5
Uniform distribution on a fair six-sided die $(p = 1/6)$
Example 6
$X \sim \text{Bern}(1/2)$, $Y$ with $(0.99, 0.01)$
$\Rightarrow\ H(X) > H(Y)$
Example 7 (Guessing game)
Q1: $P(\text{Yes}) = 1/2$, Q2: $P(\text{Yes}) = 1/4$
\[H(\text{Q1}) = -\frac12\log_2\frac12 - \frac12\log_2\frac12 = 1\ \text{bit}\] \[H(\text{Q2}) = -\frac14\log_2\frac14 - \frac34\log_2\frac34 = \frac14 \cdot 2 + \frac34\log_2\frac{4}{3} \approx 0.811278\ \text{bits}\]$\Rightarrow\ \text{Q1 is more informative}$
Example 8
\[D_1: \left(\frac19,\frac19,\frac19,\frac29,\frac29,\frac29\right), \quad D_2: \left(\frac12,\frac14,\frac18,\frac{1}{16},\frac{1}{32},\frac{1}{32}\right)\] \[H(D_1) = 3\cdot\frac{1}{9}\log_2 9 + 3\cdot\frac{2}{9}\log_2\frac{9}{2} \approx 2.503258\ \text{bits}\] \[H(D_2) = \frac12\cdot 1 + \frac14\cdot 2 + \frac18\cdot 3 + \frac{1}{16}\cdot 4 + 2\cdot\frac{1}{32}\cdot 5 = 1.9375\ \text{bits}\]$\Rightarrow\ H(D_1) > H(D_2)$
Example 9
\[x_1: (0.6,0.1,0.1,0.1,0.1), \quad x_2: (0.4,0.4,0.2,0,0)\] \[H(x_1) = 0.6\log_2\frac{1}{0.6} + 4\cdot 0.1\log_2\frac{1}{0.1} \approx 1.770951\ \text{bits}\] \[H(x_2) = 0.4\log_2\frac{1}{0.4} + 0.4\log_2\frac{1}{0.4} + 0.2\log_2\frac{1}{0.2} \approx 1.521928\ \text{bits}\]$\Rightarrow\ H(x_1) > H(x_2)$ ( $x_1$ has more uncertainty )
Example 10
\[S_1: (0.6,0.1,0.1,0.1,0.1), \quad S_2: (0.4,0.4,0.2,0,0)\] \[H(S_1) = 0.6\log_2\frac{1}{0.6} + 4\cdot 0.1\log_2\frac{1}{0.1} \approx 1.770951\ \text{bits}\] \[H(S_2) = 0.4\log_2\frac{1}{0.4} + 0.4\log_2\frac{1}{0.4} + 0.2\log_2\frac{1}{0.2} \approx 1.521928\ \text{bits}\]$\Rightarrow\ H(S_1) > H(S_2)$ ( $S_1$ is more explorative )
Example 11
Geometric distribution, $p = \frac12$, $x \ge 1$
$p_X(x) = 2^{-x}$
2.2 Properties of Entropy
long contents …..
- 1
- 2
- 3
- 4
2.3 Cross Entropy Loss
long contents …..
- e
- f
- g
- h
2.4 Jointly Distributed Random Variables
두 개의 확률변수 $X \in \mathcal{X},\ Y \in \mathcal{Y}$ 를 생각해보자. 이 확률 변수들의 결합 확률 분포(Joint Probability Distribution)의 확률 밀도 함수 (Probability mass function)는 다음과 같이 주어질 것이다.
\[p_{X, Y}(x, y)= \mathrm{Pr} [X=x, Y=y]\]이 결합확률분포의 확률밀도함수 $p_{X,Y}(x,y)$는 $X, Y$가 동시에 특정한 값 $x, y$를 가질 확률을 말한다.
이때 특정한 확률변수 하나에 대해서만 (여기서는, $X$) 그 확률을 고려해볼 수 있는데, 이를 주변 확률 분포(Marginal Probability Distribution)이라 한다. 이 값은 다음과 같이 목표가 되는 확률변수 $X=x$에서 나머지 확률변수에 대한 확률밀도함수값의 가중합으로 구해진다.
\[p_{X} (x)= \sum_{y\in \mathcal{Y} }^{}{p_{X, Y} (x, y)}\]다르게 바라보면, 다음과 같이 가능한 $y \in \mathcal{Y}$ 에 대한 조건부 확률 $p_{X\mid Y}(x\mid Y)$의 기댓값으로도 생각할 수 있고
\[p_{X} (x) = \sum_{y\in \mathcal{Y} }^{}{p_{X\mid Y} (x\mid y)p_{Y} (y)} = \mathbb{E}[p_{X\mid Y} (x\mid Y)]\]이는 $X$에 대한 주변 확률 분포(이하, Marginal)가 조건부 확률의 $Y-$평균으로 간주할 수 있음을 보여준다.
이제 결합확률분포를 이루는 두 확률변수 $X, Y$에 각각 임의의 함수$f: X\to \mathbb{R}, g: Y\to \mathbb{R}$ 을 씌웠을 때의 기댓값을 생각해보자.
\[\begin{align} \mathbb{E}[f(X)+g(Y)] &= \sum_{x,y}^{}{[f(x)+g(y)]p_{X,Y}(x,y) } \\ &= \underbrace{ \sum_{x,y}^{}{f(x)p_{X,Y}(x,y) } }_{\text{term1} } + \underbrace{ \sum_{x,y}^{}{g(y)p_{X,Y}(x,y) } }_{\text{term2} } \end{align}\]위 식에서 $\text{term1}$에서 $f$는 확률변수 $X$에만 의존하고, $\text{term2}$에서 $g$는 확률변수 $Y$에만 의존하므로 각 항을 확률변수 $Y, X$에 대한 marginal로 쓸 수 있다.
\[\begin{align} \sum_{x,y}^{}{f(x)p_{X,Y}(x,y) }+\sum_{x,y}^{}{g(y)p_{X,Y}(x,y) } &= \sum_{x}^{}{f(x)p_{X} (x)} + \sum_{y}^{}{g(y)} p_{Y} (y) \\ &= \mathbb{E}[f(X)] +\mathbb{E}[g(Y)] \end{align}\]이로써 확률변수 $X, Y$가 결합확률분포를 이룰 때, 각 변수에 대한 함수의 기댓값은 항상, 심지어 $X, Y$가 서로 독립이 아닐 때에도, $\mathbb{E}[f(X) + g(Y)] = \mathbb{E}[f(X)]+\mathbb{E}[g(Y)]$의 선형성을 띰을 알 수 있다.
결합확률분포는 또한 다음의 특징을 가진다.
\[p_{X,Y} (x,y)= p_{X} (x)\cdot p_{Y} (y) \iff X \perp\mkern-10mu\perp Y\]$\impliedby$ 방향은 독립의 정의에 의해 자연스럽게 도출된다. 따라서 $\implies$ 방향을 증명하기 위해, $\phi_{1}: X\to \mathbb{R}, \phi_{2}Y\to\mathbb{R}$인 두 함수 $\phi_{1}, \phi_{2}$에 대해
\[p_{X, Y} (x, y)= \phi_{1} (x) \cdot\ \phi_{2} (y)\]를 만족한다고 가정하자.
$X, Y$ 각각의 marginal을 조건부 확률로 나타내면,
\[\begin{align} p_{X} (x) = \sum_{y}^{}{p_{X, Y} (x, y)} = \sum_{y}^{}{\phi_{1} (x)\cdot \phi_{2} (y)} = \phi_{1} (x)\cdot \sum_{y}^{}{\phi_{2} (y)} = \phi_{1} (x) \cdot C_{Y} \\ p_{Y} (y) = \sum_{x}^{}{p_{X, Y} (x, y)} = \sum_{x}^{}{\phi_{1} (x)\cdot \phi_{2} (y)} = \phi_{2} (y)\cdot \sum_{x}^{}{\phi_{1} (x)} = \phi_{2} (y) \cdot C_{X} \end{align}\]이때, 전체 결합확률분포의 정규화 조건 $\sum_{}^{}{p_{X, Y}(x, y)}= 1$에 따라
\[\sum_{X, Y}^{}{p_{X, Y} (x, y)} = \sum_{x}^{}{}\sum_{y}^{}{} \phi_{1}(x)\cdot \phi_{2} (y) = \left( \sum_{x}^{}{\phi_{1} (x)} \right) \cdot \left( \sum_{y}^{}{\phi_{2} (y)} \right) = C_{X} \cdot C_{Y} = 1\] \[\therefore p_{X, Y} (x, y)= \cfrac{1}{C_{X} \cdot C_{Y} }\cdot \phi_{1} (x)\cdot \phi_{2} (y) = \cfrac{\phi_{1}(x)}{C_{X} }\cdot \cfrac{\phi_{2} (y)}{C_{Y} } = p_{X} (x)\cdot p_{Y} (y)\]$X, Y$가 서로 독립임을 알 수 있다.
2.4.1 Joint Entropy
결합 엔트로피(Joint Entropy)란?
결합 엔트로피 H(X1,X2)는 두 확률 변수 X1,X2가 동시에 가질 정보량의 기대값이다.
\[H(X_1, X_2) = \mathbb{E} \left[ \log \frac{1}{p_{X_1,X_2}(X_1,X_2)} \right] = \sum_{x_1,x_2} p_{X_1,X_2}(x_1,x_2) \log \frac{1}{p_{X_1,X_2}(x_1,x_2)}\]Thm. 30(Property of Entropy)
만약 $X_1$과 $X_2$가 독립이면 $H(X_1, X_2) = H(X_1) + H(X_2)$ 이다.
Proof.
\[\begin{aligned} H(X_1,X_2) &= \sum_{x_1,x_2} p_{X_1,X_2}(x_1,x_2) \log \frac{1}{p_{X_1}(x_1)p_{X_2}(x_2)} \\ &= \sum_{x_1,x_2} p_{X_1,X_2}(x_1,x_2) \left( \log \frac{1}{p_{X_1}(x_1)} + \log \frac{1}{p_{X_2}(x_2)} \right) \\ &= \sum_{x_1} p_{X_1}(x_1) \log \frac{1}{p_{X_1}(x_1)} + \sum_{x_2} p_{X_2}(x_2) \log \frac{1}{p_{X_2}(x_2)} \\ &= H(X_1) + H(X_2) \end{aligned}\]$\therefore$ 두 변수가 독립인 경우 두 변수에서 얻는 정보량은 각 변수에서 얻는 정보량의 합으로 계산
만약 X1과 X2가 강하게 상관되어 있다면, (X1,X2)로부터 얻는 정보량은 X1으로부터 얻는 정보량과 거의 비슷할 것이다.
Exercise 32
만약 $H(X_1, X_2) = H(X_1) + H(X_2)$이면, 이것이 독립을 의미하는가?
Exercise 33
Alice가 $X$를 균등분포로 ${1, 2, \dots, 8}$ 중에서 뽑고, Bob이 세 가지 Yes or No 질문을 한다.
- $X \in {5, 6, 7, 8}$ 인가?
- $X \in {1, 2, 5, 6}$ 인가?
- $X \in {1, 3, 5, 7}$ 인가?
각 $Y_i$는 베르누이 확률 변수이고, 서로 독립이다.
\[H(Y_1) = H(Y_2) = H(Y_3) = 1\] \[H(Y_1, Y_2, Y_3) = H(Y_1) + H(Y_2) + H(Y_3) = 3\] \[H(X) = \log_2 8 = 3\]$\therefore$ 세 질문으로 $X$를 완벽하게 구분할 수 있음.
2.4.2 Conditional Entropy
Conditonal Entropy란?
이미 알고 있는 정보가 존재할 때, 추가로 모르는 정보가 주는 정보량이다.
이미 알고 있는 정보 $Y$가 주어졌을 때, $X$에 관한 정보량은 \(H(X\mid Y)\)와 같이 나타내고 아래와 같이 정의된다.
\[H(X\mid Y) = \mathbb{E}\Big[\log \frac{1}{p_{X\mid Y}(X\mid Y)}\Big] = \sum_{x,y} p_{X,Y}(x,y) \log \frac{1}{p_{X\mid Y}(x\mid y)}.\]위의 경우에서 우리가 기댓값을 계산하고자 하는 함수는 $\log \frac{1}{p_{X\mid Y}(X\mid Y)}$이며 $x$ ,$y$의 확률은 joint distribution $p_{X,Y}(X,Y)$로 나타낼 수 있다.
우리는 기대값을 계산하기 위해 변수 $X$와 $Y$를 고려하고 있다. 결합 엔트로피(joint entropy)는 개별 엔트로피의 합이며, 각각의 $y$와 전체 엔트로피에 대한 각각의 기여(contribution)를 고려할 때 명확해진다. 특정 조건 y를 고정하는 경우를 생각해 보면 다음과 같이 나타낼 수 있다.
\[H(X\mid Y = y) = \mathbb{E}\Big[ \log \frac{1}{p_{X\mid Y}(X\mid Y = y)} \Big]\]이제 위 수식에서 $X$만이 유일한 변수이다. 그러므로 위 수식을 다음과 같이 나타낼 수 있다.
\[= \sum_{x} p_{X\mid Y}(x\mid y) \log \frac{1}{p_{X\mid Y}(x\mid y)}\]만약 우리가 특정 조건 $y$에 대한 모든 가능한 조건부 엔트로피를 합하면, $Y$에 주어진 $X$의 전체 조건부 엔트로피를 다음과 같이 나타낼 수 있다
\[H(X\mid Y) = \sum_{y} p_Y(y) H(X\mid Y = y)\]이제 엔트로피 $H(X)$와 $H(Y\mid X)$를 고려해보자. $H(X)$는 $X$에 대한 정보이고, $H(Y\mid X)$는 $X$의 정보가 주어졌을 때 $H(X,Y)$에서의 ‘남은’정보이다. 따라서 우리는 $H(X) + H(Y\mid X) = H(X,Y)$라고 기대할 수 있고 아래와 같이 증명가능하다.
\[\mathbb{E}\Big[ \log \frac{1}{p_X(X)} \Big]+ \mathbb{E}\Big[ \log \frac{1}{p_{Y\mid X}(Y\mid X)} \Big]= \mathbb{E}\Big[ \log \frac{1}{p_X(X) p_{Y\mid X}(Y\mid X)} \Big]\] \[= \mathbb{E}\Big[ \log \frac{1}{p_{X,Y}(X,Y)} \Big]\] \[= H(X,Y).\]$p_{Y\mid X}(Y\mid X) = \frac{p_{X,Y}(X,Y)}{p_X(X)}$ 를 이용하면 위 증명이 성립함을 쉽게 알 수 있다.
Exercise 35. 위의 추론 게임(guess game)에서 다음을 계산하여라
- $H(Y2\mid Y1)$
- $H(Y4\mid Y1)$
풀이:
- $\mathbb{E}\Big[ \log \frac{1}{p_{Y2\mid Y1}(Y2\mid Y1)} \Big]$을 구하면 된다.
이 경우에서는 $Y1$과 $Y2$가 독립이므로 $\mathbb{E}\Big[ \log \frac{1}{p_{Y2}(Y2)} \Big]$를 구하면 된다.
즉, $\sum_{y} p_{Y2}(y) \log \frac{1}{p_{Y2}(y)}$를 계산하면 된다.
답: 1
2.
$p_{}(Y4=0\mid Y1=0) = 3/4$
$p_{}(Y4=1\mid Y1=0) = 1/4$
$p_{}(Y4=0\mid Y1=1) = 1/4$
$p_{}(Y4=1\mid Y1=1) = 3/4$
를 이용하면 $H(Y4\mid Y1=0)$은 $3/4\log4/3+1/4\log4$이고
$H(Y4\mid Y1=1)$은 $3/4\log4/3+1/4\log4$이다.
따라서 $H(Y4\mid Y1)$은 ($1/2$)($3/4\log4/3+1/4\log4$)+($1/2$) ($3/4\log4/3+1/4\log4$)이다.
이를 $H(Y4)=1$와 비교해보면 더 작은 것을 알 수 있다.
따라서 조건이 존재할 경우 정보가 같거나 줄어든다는 사실을 알 수 있다.
2.4.3 Mutual Information
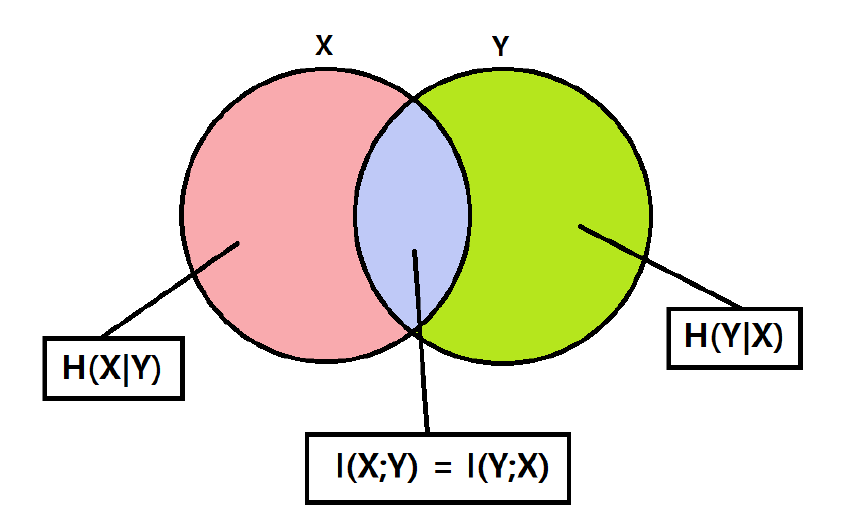
상호 정보량(Mutual Information)이란?
상호 정보량은 엔트로피와 조건부 엔트로피의 차이로 정의된다.
\[I(X; Y) = H(X) - H(X \mid Y), \quad I(Y; X) = H(Y) - H(Y \mid X)\]조건부 엔트로피와 상호 정보량의 관계는 위와 같은 도식으로도 표현 가능하다. 특히 $I(X; X)$의 경우 아래와 같이 계산되며, 결과적으로 $H(X)$와 같다.
\[\begin{align*} I(X; X) &= H(X) - H(X \mid X) \\ &= H(X) \end{align*}\]만약 $X$와 $Y$가 서로 독립이라면, 위 도식 혹은 정의에 의해 \(I(X; Y) = 0\)임을 보일 수 있다.
또한, $I(X; Y) = 0$이면 $X$와 $Y$는 독립이다.
상호 정보량은 다음과 같이 KL divergence로도 표현된다.
\[I(X; Y) = D(p_{X,Y} \parallel p_X p_Y)\]위 식에서 볼 수 있듯이, 상호 정보량은 두 확률 분포 간의 거리 또는 발산 정도를 의미한다. $I(X; Y) = 0$이라면, $p_{X,Y} = p_X p_Y$가 되어 $X$와 $Y$는 독립이 된다.
2.4.4 Properties of Mutual Information
정리 36 (데이터 처리 부등식 I) 정리. $f$가 결정론적 함수라면,
\[H(X) \ge H(f(X))\]이다.
증명.
\[H(X, f(X)) = H(X) + H(f(X)\mid X) = H(X)\]또한,
\[H(X, f(X)) = H(f(X)) + H(X\mid f(X)) \ge H(f(X))\]따라서 $H(X) \ge H(f(X))$이다.
($f$가 일대일 대응이고 전사이면 역함수가 존재하므로 이 경우에는 $H(X)=H(f(X))$.)
정리 37 (Mutual information은 대칭적이다) 정리.
\[I(X;Y) = I(Y;X)\]증명.
\[\begin{aligned} I(X;Y) &= H(X) - H(X\mid Y) \\ &= H(X) - \bigl(H(X,Y) - H(Y)\bigr) \\ &= H(X) + H(Y) - H(X,Y) \\ &= I(Y;X) \end{aligned}\]정리 38 (Mutual information은 비음수이다)
정리.
증명.
\[\begin{aligned} H(X) - H(X\mid Y) &= \mathbb{E}\left[\log \frac{1}{p_X(X)}\right] - \mathbb{E}\left[\log \frac{1}{p_{X\mid Y}(X\mid Y)}\right] \\ &= \mathbb{E}\left[\log \frac{p_{X\mid Y}(X\mid Y)}{p_X(X)}\right] \\ &= \mathbb{E}\left[\log \frac{p_{X,Y}(X,Y)}{p_X(X)p_Y(Y)}\right] \\ &= \sum_{x,y} p_{X,Y}(x,y) \log \frac{p_{X,Y}(x,y)}{p_X(x)p_Y(y)} \\ &= D\!\left(p_{X,Y} \,\|\, p_X p_Y\right) \ge 0 \end{aligned}\]따라서 $I(X;Y) = D(p_{X,Y}\,|\,p_X p_Y) \ge 0$.
여기서 $p_X p_Y$는 $X$와 $Y$가 각각의 주변분포 $p_X, p_Y$를 가지지만 서로 독립인 $(X,Y)$에 대한 분포이다.
또한 부등식 $H(X) \ge H(X\mid Y)$는 “조건부를 취하면 (불확실성이) 줄어들거나 유지된다”는 해석을 가질 수 있다.
정리 39 (데이터 처리 부등식 II) 정리. 임의의 함수 $f: \mathcal{X} \to \mathbb{R}$에 대해 다음이 성립한다:
\[I(X;Y) \ge I(f(X);Y)\]증명.
\[\begin{aligned} I(X;Y) &= H(Y) - H(Y\mid X) \\ &= H(Y) - H(Y\mid X, f(X)) \\ &\ge H(Y) - H(Y\mid f(X)) \\ &= I(f(X);Y) \end{aligned}\]일반화.
$X - Y - Z$가 마르코프 체인(또는 $X$와 $Z$가 $Y$를 조건으로 주었을 때 조건부 독립)일 때, 다음이 서로 동치이다:
- $X - Y - Z \iff X$와 $Z$가 $Y$를 주었을 때 독립이다. $(X \perp Z \mid Y)$
- $Y$가 알려져 있을 때 $X$는 $Z$를 추정하는 데 쓸모없다.
- 모든 $x,y,z$에 대해 $p_{Z\mid X,Y}(z\mid x,y) = p_{Z\mid Y}(z\mid y)$.
정리 40 (데이터 처리 부등식 III)
정리.
만약 $X - Y - Z$가 마르코프 체인을 이룬다면,
또는 대칭적으로 $I(Z;X) \le I(Z;Y)$.
증명.
\[\begin{aligned} I(Y;Z) &= H(Z) - H(Z\mid Y) \\ &= H(Z) - H(Z\mid X, Y) \\ &\ge H(Z) - H(Z\mid X) \\ &= I(X;Z) \end{aligned}\]따라서 $I(Y;Z) \ge I(X;Z)$, 즉 $I(Z;Y) \ge I(Z;X)$이다.
문제 29.(b)
$X, Y, Z$가 결합 확률 분포를 가지는 임의의 확률 변수일 때, 다음 부등식을 증명하고 등호 성립 조건을 찾아라.
(b) $I(X, Y; Z) \ge I(X; Z)$.
풀이
1. 체인 룰(chain rule) 적용 상호 정보의 체인 룰에 따르면:
\[I(X, Y; Z) = I(X; Z) + I(Y; Z \mid X).\]이는 “$X, Y$가 합쳐질 때 $Z$와 주고받는 정보량”을
먼저 $X$가 주는 정보량과, $X$를 알고 난 뒤 $Y$가 더 주는 추가 정보량으로 분해한 식이다.
2. 조건부 상호 정보의 비음성 항상
\[I(Y; Z \mid X) \ge 0\]이다. (KL 발산 형태로 증명할 수 있다.)
3. 부등식 결론 따라서
\[I(X, Y; Z) = I(X; Z) + I(Y; Z \mid X) \ge I(X; Z).\]4. 등호 성립 조건 등호 $I(X, Y; Z) = I(X; Z)$가 되려면
\[I(Y; Z \mid X) = 0 \iff Y \perp Z \mid X\]이어야 한다.
즉 “$X$를 조건으로 두었을 때 $Y$와 $Z$가 독립”이어야 한다.
이 역시 $Y \to X \to Z$ 형태의 마르코프 사슬과 동치이다.
문제 31. 임의의 결정론적 함수 $g$에 대하여,
\[H(X \mid g(Y)) = H(X \mid Y)\]이 성립하려면 어떤 조건이 필요한가?
풀이
1. 데이터 처리 부등식 I (조건부 형태)
이미 알고 있는 바:
왜냐하면 “$Y$를 알면 $g(Y)$를 알 수 있지만, $g(Y)$를 안다고 해서 항상 $Y$가 복원되지는 않으므로” 불확실성이 더 작아지거나 같기 때문이다.
2. 등호 조건 분석
\[H(X \mid g(Y)) = H(X \mid Y)\]일 때, 양쪽 사이에 끼어 있는
\[H(X \mid Y) - H(X \mid g(Y)) = I(X;Y \mid g(Y)) = 0\]이다.
즉, “$g(Y)$를 조건으로 $X$와 $Y$가 독립”이어야 한다.
3. 마르코프 사슬 해석
\[I(X;Y \mid g(Y)) = 0 \iff X \perp Y \mid g(Y).\]이는 바로
\[X \longrightarrow g(Y) \longrightarrow Y\]꼴의 마르코프 사슬 형태가 성립함을 뜻한다.
4. 특수 사례
- $g$가 일대일 대응(가역)이면 당연히 $g(Y) \leftrightarrow Y$ 양방향 복원이 가능하므로 등호 성립.
- 또 $X$와 $Y$가 본래 독립이라도
\(H(X \mid g(Y)) = H(X) = H(X \mid Y)\)
이므로 등호가 된다.
이 두 경우는 포함되지만, 유일한 경우는 아니다.
문제 42.(b)
다음 부등식들 중 일반적으로 $ \ge, =, \le $ 중 어느 관계가 성립하는지 각각 표시하라.
(b) $I(g(X); Y)$ vs. $I(X; Y)$.
풀이
1. 데이터 처리 부등식 II 이것은 4.4절에서 나온 정리와 같다. 임의의 결정론적 함수 $g$에 대하여:
\[I(g(X); Y) \le I(X; Y).\]2. 직관
- $X$가 $Y$에 갖는 정보량이 $I(X;Y)$이고,
- $X$를 $g$로 가공한 $g(X)$는 $X$보다 “덜 상세”(또는 같음) →
- $g(X)$가 $Y$에 제공할 수 있는 정보도 당연히 $I(X;Y)$ 이하여야 한다.
3. 형식적 증명
\[\begin{aligned} I(g(X); Y) &= H(Y) - H(Y \mid g(X)) \\ &\le H(Y) - H(Y \mid X) \quad (\text{조건부 엔트로피 감소 } H(Y \mid g(X)) \ge H(Y \mid X)) \\ &= I(X; Y). \end{aligned}\]4. 등호 성립 조건 등호가 되려면
\[H(Y \mid g(X)) = H(Y \mid X) \iff I(Y; X \mid g(X)) = 0 \iff Y \perp X \mid g(X).\]즉 “$g(X)$를 조건으로 $X$와 $Y$가 독립”일 때 등호가 된다.
다시 말해 $g(X)$를 기준으로 $X$와 $Y$는 더 이상의 상호 정보(조건부)가 없다.
2.4.5 Conditional Mutual Information
조건부 상호정보량이란?
조건부 상호정보량은 변수 $Y$가 주어졌을 때, $X$와 $Z$ 사이의 상호정보량을 의미한다.
\[I(X; Z \mid Y) = H(X \mid Y) - H(X \mid Y, Z)\]또는 다음과 같이도 표현된다.
\[I(X; Z \mid Y) = H(Z \mid Y) - H(Z \mid Y, X)\]이는 $Z$를 알면 $X$의 불확실성이 얼마나 줄어드는지를 나타낸다.
조건부 상호정보량이 0이 되는 조건
조건부 상호정보량이 0이 되려면, $X$와 $Z$가 $Y$가 주어졌을 때 조건부 독립이어야 한다.
\[P(X, Z \mid Y) = P(X \mid Y) \cdot P(Z \mid Y)\]이는 마코프 체인 구조인 $X \rightarrow Y \rightarrow Z$와 동일하다.
[!warning] 조건부 상호정보량 $I(X; Z \mid Y)$ 와 일반 상호정보량 $I(X; Z)$는 일반적으로 관계가 없다.
예시 1: 조건부 상호정보량이 일반 상호정보량보다 클 수 있다.
\[I(X; Z \mid Y) > I(X; Z)\]- $X \in {0, 1}$, $Z \in {0, 1}$
- 각 확률은 다음과 같다:
- $Y = X \oplus Z$ (XOR 연산)
이 경우 다음이 성립한다:
\[I(X; Z) = 0, \quad I(X; Z \mid Y) = 1\]즉, 조건 없이 보면 $X$와 $Z$는 독립이지만, $Y$를 알면 종속이 된다.
예시 2: 일반 상호정보량은 존재하지만 조건부 상호정보량은 0인 경우
\[I(X; Z) > 0, \quad I(X; Z \mid Y) = 0\]이는 마코프 체인 $X \rightarrow Y \rightarrow Z$ 구조에서 발생한다.
여러 변수에 대한 상호정보량
두 변수 $X, Y$ 와 $Z$ 사이의 상호정보량은 다음과 같이 체인 룰로 나눌 수 있다.
\[I(X, Y; Z) = I(X; Z) + I(Y; Z \mid X)\]상호정보량의 체인 분해
여러 변수 $X_1, X_2, \dots, X_n$ 과 $Y$ 간의 상호정보량은 다음과 같이 분해된다.
\[I(X_1, X_2, \dots, X_n; Y) = I(X_1; Y) + I(X_2; Y \mid X_1) + I(X_3; Y \mid X_1, X_2) + \dots\]또는 일반화하여 다음과 같이 표현된다:
\[I(X_n; Y) = \sum_{i=1}^{n} I(X_i; Y \mid X_1, \dots, X_{i-1})\]2.5 Random Process
확률 과정(Random Process)이란?
확률 과정은 다음과 같이 정의됩니다:
\[X = \{X_n\}_{n=1}^{\infty}\]이것은 순서를 가진 확률 변수들의 집합이며, 각 $X_n$은 특정 확률 분포를 따릅니다.
- 여기서 $n$은 꼭 시간(time)을 의미하지 않아도 됩니다.
- 예시:
- 텍스트: $X_1$은 첫 번째 문자, $X_2$는 두 번째 문자 등
- 이미지: $X_{i,j}$는 $i$행 $j$열 픽셀의 밝기
- 시계열: $X_t$는 $t$초 후의 값
핵심: 인덱스가 시간일 필요는 없으며, 순서만 있으면 확률 과정이 됩니다.
i.i.d. 과정이란?
i.i.d.는 independent and identically distributed의 약자입니다.
- 독립(independent): 각 $X_n$이 서로 영향을 주지 않음
- 동일 분포(identically distributed): 모든 $X_n$이 동일한 확률 분포를 따름
전체 확률은 다음처럼 단순 곱으로 계산할 수 있습니다:
\[P(X_1 = x_1, \dots, X_n = x_n) = \prod_{i=1}^{n} P(X_i = x_i)\]현실은 대부분 i.i.d.가 아님 예: 텍스트
- “progra_ing”이라는 단어에서 빈칸에 ‘m’이 올 가능성이 높다고 판단할 수 있음
- 이는 앞뒤 문맥이 영향을 주기 때문 → 요소들 간에 의존성 존재
$\therefore$ 현실의 데이터는 보통 독립적이지 않고, 앞뒤 요소에 영향을 받습니다.
i.i.d.가 아닌 경우 사용하는 모델들:
- 마르코프 모델 (Markov Model)
- 순환 신경망 (Recurrent Neural Network, RNN)
- 트랜스포머 (Transformer)
2.5.1 What is Markovian?
i.i.d. ←────────────|────────────→ Practical 1st-order Markov
1차 마르코프 체인(first-order Markov chain)의 개념은, i.i.d. 가정과 실제 현실에서의 데이터 구조 사이를 연결해주는 중간 다리 역할을 합니다. “마르코프(Markov)”라는 말은 1차 상관성(first-order correlation)이 있다는 의미입니다. 즉, 현재 상태는 직전 상태에만 의존하고, 그 이전의 상태에는 의존하지 않는다는 것입니다.
예제 41: 랜덤 워크(Random Walk)
확률 과정 $X = {X_n}$를 다음과 같이 정의합니다:
초기 상태:
\[X_0 = 0\]이후 각 $n$에 대해:
\[X_n = \begin{cases} X_{n-1} + 1 & \text{with probability } \frac{1}{2} \\ X_{n-1} - 1 & \text{with probability } \frac{1}{2} \end{cases}\]즉, 현재 위치에서 매 스텝마다 동전 던지기로 1만큼 앞 또는 뒤로 이동하는 무작위 행보입니다.
예를 들어 다음과 같은 정보가 주어졌다고 해 봅시다:
\[X_{101} = 51\]이때 $X_{102}$는 다음 두 가지 중 하나입니다:
- $X_{102} = 50$
- $X_{102} = 52$
추가로 $X_{100} = 50$이라는 정보를 안다고 해도, $X_{102}$가 어떻게 될지를 예측하는 데 아무런 도움이 되지 않습니다.
이것은 1차 마르코프 체인의 특성과 정확히 일치합니다:
미래 상태는 현재 상태에만 의존하며, 과거는 무시됩니다.
핵심 요약
| 구분 | 설명 |
|---|---|
| i.i.d. | 각 값이 서로 독립이고 동일한 분포를 가짐 |
| 1차 마르코프 | 현재 상태는 바로 직전 상태에만 의존함 |
| 현실 데이터 | 대부분 i.i.d.는 아니며, 1차 마르코프 모델이 더 현실적 |
| 랜덤 워크 예시 | $X_{n}$은 $X_{n-1}$만으로 결정되며, $X_{n-2}$는 영향을 주지 않음 |
요약 구조
i.i.d. ←────────────|────────────→ 현실 데이터 ↑ 1st-order Markov (현재 상태는 직전 상태에만 의존)
2.5.2 1st Order Markov Process
1차 마르코프 과정이란? 확률 과정 $X$ = ${X_1, X_2, \dots, X_n}$이 있다고 할 때, $P(X_i \mid X_{i-1}, X_{i-2}, \dots, X_1) = P(X_i \mid X_{i-1})$를 만족하는 과정을 1차 마르코프 과정이라고 한다.
$\therefore$ 현재 상태 $X_i$는 직전 상태 $X_{i-1}$에만 의존하고, 그 이전 상태들과는 무관하다.
\[P(X_1, X_2, \dots, X_n) = P(X_1) \times P(X_2 \mid X_1) \times \cdots \times P(X_n \mid X_{n-1})\]모든 가능한 sequence tuple들의 결합 확률 분포를 $P_{X^n}(x^n) = P_{X_1, \cdots, X_n}(x_1, \dots, x_n)$라고 할 때, 1차 마르코프 과정은 다음을 만족한다.
$>P_{X^n}(x^n) = \prod_{i=1}^n P_{X_i \mid X_{i-1}}(x_i \mid x_{i-1})$
1차 마르코프 과정이므로,
\[P(X_i \mid X_{i-1}, X_{i-2}, \dots, X_1) = P(X_i \mid X_{i-1})\]위 식을 바꾸어 쓰면,
\[P(X_1, X_2, \dots, X_n) = P(X_1) \prod_{i=2}^n P(X_i \mid X_{i-1})\]상태 공간이 ${1, \dots, n}$이고 전이 확률이 동일하다고 가정하면, 전이 행렬 $P$를 정의할 수 있다.
\[P_{u,v} = \Pr[X_i = u \mid X_{i-1} = v]\]그리고 $t$시점 상태 분포 벡터를
\[\pi_t = \begin{bmatrix} \Pr[X_t = 1] \\ \Pr[X_t = 2] \\ \vdots \\ \Pr[X_t = n] \end{bmatrix}\]라고 하면, 각 상태 u에 대해 다음 식이 성립한다.
\[\Pr[X_t = u] = \sum_{v=1}^n \Pr[X_t = u \mid X_{t-1} = v] \Pr[X_{t-1} = v] = \sum_{v=1}^n P_{u,v} \pi_{t-1,v}\]이를 벡터 형태로 변환하면
\[\pi_t = P \times \pi_{t-1}\]\[P_{X_i \mid X_{i-1}}(0 \mid 1) = P_{X_i \mid X_{i-1}}(1 \mid 0) = \alpha < \frac{1}{2}\] \[P_{X_i \mid X_{i-1}}(1 \mid 0) = P_{X_i \mid X_{i-1}}(0 \mid 1) = 1 - \alpha\]Exercise 43. 이진확률과정 $X$를 고려해보자. 전이 확률이 다음과 같이 주어진다.
이때, 전이 행렬 $P$는 다음과 같이 정의할 수 있다
\[P = \begin{bmatrix} 1 - \alpha & \alpha \\ \alpha & 1 - \alpha \end{bmatrix} \quad (115)\]초기 상태 분포를 다음과 같이 정의하면,
\[\pi_0 = [1, 0]\]다음 단계 상태 분포 $\pi_1$은 다음과 같다.
\[\pi_1 = [1 - \alpha, \alpha]\]2.5.3 kth Order Markov Process
확률 과정 X에 대해,
\[P_{X_i | X^{i-1}}(x_i \mid x^{i-1}) = P_{X_i | X_{i-k}^{i-1}}(x_i \mid x_{i-k}^{i-1}),\]이 성립하는 시퀀스는 k차 마르코프 과정(kth Order Markov Process)를 따른다.
즉, k차 마르코프 과정을 따르는 시퀀스에 대해서
\[P_{X^n}(x^n) = \prod_{i=1}^{n} P_{X_i \mid X_{i-k}^{i-1}}(x_i \mid x_{i-k}^{i-1})\]이 성립한다.
2.5.4 Stationary Distribution
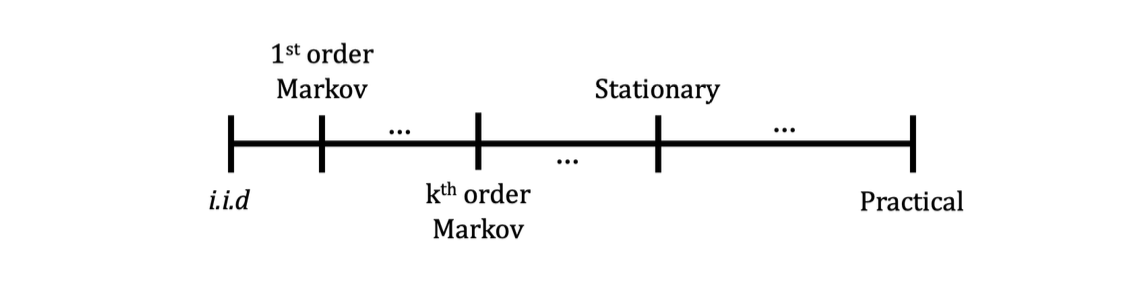
그림 7 설명
- i.i.d(독립 동일 분포) 가정: 시퀀스 내 각 확률변수가 서로 완전히 독립이며 상관관계가 없음.
- 실제(practical) 환경: 시퀀스 내 변수들 간의 상관관계가 높음.
- 정상 분포(stationary distribution): i.i.d보다 현실을 더 잘 근사하며, $k$차 마르코프 과정보다 현실 상황에 더 가까움.
정의 45. 정상(stationary) 과정
랜덤 프로세스 $X_1, X_2, \dots, X_n$이 다음을 만족하면 정상 과정이라 한다.
- 임의의 $n$-튜플을 $i$번째 시점에서 시작해도, $(i+1)$번째 시점에서 시작해도 분포가 동일하다.
- 확률변수의 분포가 시간에 의존하지 않는다.
여기서
- $P_{X_i^n}$ : $i$번째 시점부터 $n$개의 변수를 포함하는 분포
- $P_{X_{i+1}^n}$ : $(i+1)$번째 시점부터 $n$개의 변수를 포함하는 분포
예제 46. 랜덤 워크(Random Walk)
\[X_0 = 0,\quad X_n = X_{n-1} \pm 1\]- $X_1$의 가능한 값: ${0, -1}$
- $X_2$의 가능한 값: ${2, 0, -2}$
시간이 지남에 따라 값의 분포가 변하고, $X_n$이 $X_0$보다 “더 랜덤”해진다.
⇒ 정상이 아님.
비고
- 모든 마르코프 과정이 정상인 것은 아니다.
- 정상 과정은 무한 의존성(infinite dependency)을 가질 수 있다.
2.5.5 Stationary Markov Process
예제 47. 초기 분포가 $P(A) = P(B) = P(C) = \frac{1}{3}$인 다음 1차 마르코프 과정을 생각해보자.
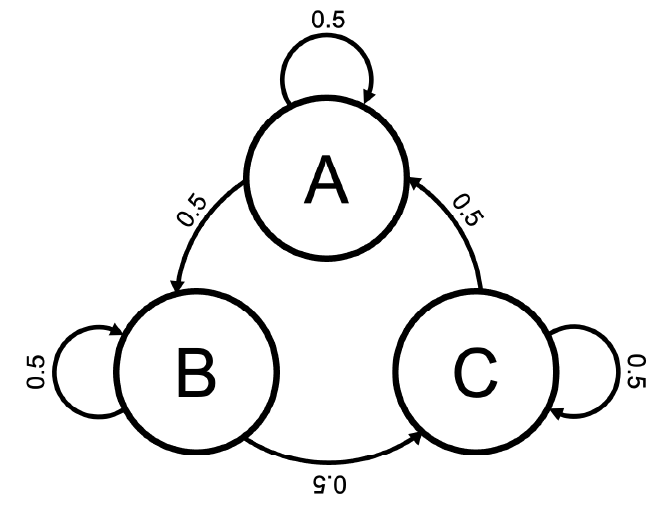
각 전이 확률이 위와 같으면,
\[\begin{aligned} P(X_1 = A) &= P(X_1 = B) = P(X_1 = C) = \frac{1}{3} \\ P(X_2 = A) &= P(X_1 = A) \cdot P(X_2 = A|X_1 = A) \\ &\quad + P(X_1 = C) \cdot P(X_2 = A|X_1 = C) = \frac{1}{3} \end{aligned}\]이며 같은 방식으로 $P(X_2 = B)$, $P(X_2 = C)$도 모두 $\frac{1}{3}$이 된다.
이를 $X_3, X_4, \dots$까지 확장해도 확률 분포가 변하지 않으며, 항상 $\frac{1}{3}$을 유지하게 된다.
즉 이는 정상(stationary) 과정인 것이다.
예제 48. 예제 47과 같은 마르코프 과정에서 초기 분포만 $P(X_1 = A) = 1$, $P(X_2 = A) = P(X_2 = B) = \frac{1}{2}$인 상황을 생각해보자. 이 경우 확률 분포가 시간에 따라 바뀌므로 더 이상 정상(stationary)이 아니다. 즉 마르코프 과정이 항상 정상인 것은 아니며, 정상이 되기 위해선 특정 조건을 만족해야 한다.
정리 49. 유한 상태(finite state), 가역성(irreducible), 비주기성(aperiodic)을 만족하는 경우, 마르코프 과정은 정상 분포(stationary distribution)를 가질 수 있다.
예제 50. $p_{X_i \mid X_{i-1}}(1\mid0) = p_{X_i \mid X_{i-1}}(0 \mid 1) = \alpha < \frac{1}{2}, p_{X_i \mid X_{i-1}}(0 \mid 0) = p_{X_i \mid X_{i-1}}(1 \mid 1) = 1 - \alpha$ 인 이항 확률 과정을 생각해보자. 이 때 전이 행렬은 다음과 같다.
\[P = \begin{pmatrix} 1 - \alpha & \alpha \\ \alpha & 1 - \alpha \end{pmatrix}\]초기 분포를 $\pi_0 = [1/2, 1/2]$라고 하면, 모든 시점 $t$에 대해 $\pi_t = [1/2, 1/2]$로 유지된다.
즉, 정상 분포 $\pi^*$는 다음 조건을 만족한다.
따라서 정상 분포는 전이 행렬 $P$의 고유값 1에 해당하는 고유벡터가 된다. (행렬 $P$의 고유값 $\lambda$는 $\det(P - \lambda I) = 0$의 해라는 것을 기억하자.)
예제 51. 전이 행렬 $P$가 대칭(symmetric)일 경우, 균일 분포(uniform distribution)는 정상 분포가 됨을 보여라.
풀이: $\pi^\star = \begin{bmatrix} 1/n, 1/n, \cdots, 1/n \end{bmatrix}^\top$라 하자. $\pi^\star$가 정상 분포이려면 $P \pi^\star = \pi^\star$을 만족해야 한다.
\[[P\pi^\star]_i = \sum_{j=1}^n P_{ij} \cdot \pi^\star_j = \sum_{j=1}^n P_{ij} \cdot \frac{1}{n} = \frac{1}{n} \sum_{j=1}^n P_{ij}\]여기서 $P$가 대칭, 즉 $P_{ij} = P_{ji}$이므로
\[[P\pi^\star]_i = \frac{1}{n} \sum_{j=1}^n P_{ji}\]전이 행렬에서 한 행의 합은 확률 분포이므로 항상 1이 되어 $[P\pi^\star]_i = 1/n$. 따라서 $P \pi^\star = \pi^\star$, $\pi^\star$는 정상 분포이다.
만약 다음이 존재한다면 우리는 $\pi_\infty$를 극한 분포(limiting distribution)라 한다.
\[\pi_\infty = \lim_{t \to \infty} \pi_t\]정리 52. 극한 분포는 정상 분포여야 한다.
풀이: $\pi_{t+1} = P \pi_t$ 의 양변에 극한을 취하여 쉽게 증명 가능하다.
예제 53. 이산 확산(Discrete Diffusion) $X_0 \sim p_0$라 할 때, 다음과 같은 전이 행렬을 가진 1차 마르코프 과정을 생각해보자.
\[P = \begin{bmatrix} 1 - \epsilon & \epsilon/(n-1) & \cdots & \epsilon/(n-1) \\ \epsilon/(n-1) & 1 - \epsilon & \cdots & \epsilon/(n-1) \\ \vdots & \vdots & \ddots & \vdots \\ \epsilon/(n-1) & \epsilon/(n-1) & \cdots & 1 - \epsilon \end{bmatrix}\]극한 분포는 균일 분포 $\pi^\star = \begin{bmatrix} 1/n, 1/n, \cdots, 1/n \end{bmatrix}^\top$이며( $\because$ 정리 52, 예제 51), 충분히 큰 $N$에 대해 $\pi_N \approx \pi^\star$이라 할 수 있다. 반대로, 우리가 어떤 시점 $t$에 대해 $X_{t+1}$에서 $X_t$를 복원하는 신경망 $f_\theta$를 학습할 수 있다고 하자:
\[X_t \approx f_\theta(X_{t+1}, t)\]그렇다면 우리는 균일 분포로부터 $\tilde X_N$을 샘플링한 후, $f_\theta(\cdot, t)$ 를 재귀적으로 적용하여 $\tilde X_0$ 를 얻을 수 있다. 이 $\tilde X_0$는 $X_0 \sim p_0$와 유사하게 동작할 것으로 기대할 수 있으며, 이것이 생성적 확산 모델(generative diffusion process)의 핵심 아이디어이다.
2.6 Continuous Random Variables
2.6.1 Probability Density Function
2.6.2 Gaussian
정의 54. 단일 가우시안 분포
평균이 $\mu$, 분산이 $\sigma^2$인 가우시안 분포를 $X \sim \mathcal{N}(\mu, \sigma^2)$라고 하며, 확률밀도함수(pdf)는 다음과 같다.
정의 55. 2차원(이변량) 가우시안 분포
$X_1, X_2$가 평균 $\mu = (\mu_1, \mu_2)$, 공분산 행렬
를 가지면, $(X_1, X_2) \sim \mathcal{N}(\mu, \Sigma)$라 하고, 결합 확률밀도함수(pdf)는
\[f_{X_1, X_2}(x_1, x_2) = \frac{1}{(2\pi)^2 \det(\Sigma)} \exp\left( -\frac{1}{2} (x - \mu)^\top \Sigma^{-1} (x - \mu) \right),\]여기서 $x = (x_1, x_2)$이다.
정리 56. 조건부 분포의 가우시안성
$(X_1, X_2) \sim \mathcal{N}(\mu, \Sigma)$이면, $X_1 \mid X_2$도 가우시안이며,
-
조건부 평균:
\[\mathbb{E}[X_1 \mid X_2 = x_2] = \mu_1 + \frac{\sigma_{12}}{\sigma_{22}} (x_2 - \mu_2)\] -
조건부 분산: \(\mathrm{Var}(X_1 \mid X_2) = \sigma_{11} - \frac{\sigma_{12}\sigma_{21}}{\sigma_{22}}\)
여기서
\[\Sigma = \begin{pmatrix} \sigma_{11} & \sigma_{12} \\ \sigma_{21} & \sigma_{22} \end{pmatrix}\]정의 57. $n$차원(다변량) 가우시안 분포
$X_n = (X_1, X_2, \dots, X_n)$이 평균 $\mu = (\mu_1, \mu_2, \dots, \mu_n)$, 공분산 행렬 $\Sigma$를 가지면,
$X_n \sim \mathcal{N}(\mu, \Sigma)$라 하고, 결합 확률밀도함수(pdf)는
이다.
성질
독립 가우시안 $X_1 \sim \mathcal{N}(\mu_1, \sigma_1^2)$, $X_2 \sim \mathcal{N}(\mu_2, \sigma_2^2)$에 대해,
합 $X_1 + X_2$도 가우시안이며,
정리 58. 선형 변환의 가우시안성
$X_n$이 가우시안 벡터이면, 임의의 행렬 $A \in \mathbb{R}^{m \times n}$에 대해
또한 가우시안 벡터이다.
2.6.3 Differential Entropy
이산(discrete)적인 상황에서는, 확률 분포가 균일(uniform)할 때 엔트로피가 최대가 된다. 그리고 사건(event)의 개수가 많아질수록 엔트로피가 증가한다. 그러나 이를 연속(continuous) 적인 상황으로 확장하기 위해서는 해결해야 할 몇 가지 문제가 있다. 때문에 우리는 일단 연속 확률 변수의 상호정보량을 정의해야 하며, 이에 앞서 KL 발산(KL divergence) 의 정의를 연속적인 상황으로 확장하면 다음과 같다.
\[D(f \parallel g) = \mathbb{E}_f \left[ \log \frac{f(X)}{g(X)} \right]\]이산적인 상황과 마찬가지로, KL 발산은 항상 0 이상이다.
\[\begin{aligned} D(f \parallel g) &= \mathbb{E}_f \left[ \log \frac{f(X)}{g(X)} \right] \\ &= \int f(x) \cdot \log \frac{f(x)}{g(x)} \, dx \\ &= - \int f(x) \cdot \log \frac{g(x)}{f(x)} \, dx \\ &\ge - \log \left( \int f(x) \cdot \frac{g(x)}{f(x)} \, dx \right) \\ &= 0 \end{aligned}\]$-\log$는 아래로 볼록(convex)인 함수이므로, Jensen 부등식을 위와 같이 적용할 수 있다.
이제 우리는 KL 발산을 통해 연속적인 상황에서의 상호정보량을 다음과 같이 정의한다.
\[\begin{aligned} I(X; Y) &= \mathbb{E} \left[ \log \frac{f_{X,Y}(X,Y)}{f_X(X) f_Y(Y)} \right] \\ &= D\left(f_{X,Y} \parallel f_X f_Y \right) \end{aligned}\]정리 59. 상호정보량은 양수이다
\[I(X; Y) \ge 0\]이는 $h(X) \ge h(X \mid Y)$를 의미하며, 조건부를 취하는 것은 미분 엔트로피를 감소(또는 최소 유지)시킨다는 것을 알 수 있다.
매우 작은 $\Delta$에 대해 $P(X^\Delta) = P(i \cdot \Delta \le X \le (i+1) \cdot \Delta) = \Delta \cdot f_X(X)$로 연속 확률변수 $X, Y$를 $X^\Delta, Y^\Delta$로 이산화(discretize)하면, 상호정보량의 정의는 다음과 같다.
\[\begin{aligned} I(X^\Delta; Y^\Delta) &= \mathbb{E} \left[ \log \frac{P_{X^\Delta, Y^\Delta}(X^\Delta, Y^\Delta)}{P_{X^\Delta}(X^\Delta) P_{Y^\Delta}(Y^\Delta)} \right] \\ &= \mathbb{E} \left[ \log \frac{\Delta^2 \cdot f_{X,Y}(X,Y)}{\Delta \cdot f_X(X) \cdot \Delta \cdot f_Y(Y)} \right] \\ &= \mathbb{E} \left[ \log \frac{f_{X,Y}(X,Y)}{f_X(X) \cdot f_Y(Y)} \right] \end{aligned}\]이와 같이, 우리는 이산적인 상황으로부터 연속적인 상황에서 상호정보량의 정의를 자연스럽게 도출할 수 있다.
미분 엔트로피(differential entropy) $h$는 이산 확률변수의 엔트로피에 대응하는 연속 확률변수의 엔트로피이다. 위와 동일한 전략을 사용하여 연속 엔트로피를 유도해보며, 어떠한 차이가 있는지 살펴보자.
\[\begin{aligned} H(X^\Delta) &= \mathbb{E} \left[ \log \frac{1}{P_{X^\Delta}(X^\Delta)} \right] \\ &= \mathbb{E} \left[ \log \frac{1}{\Delta \cdot f_X(X)} \right] \\ &= \mathbb{E} \left[ \log \frac{1}{f_X(X)} \right] - \log \Delta \\ &= h(X) - \log \Delta \end{aligned}\]여기서
\[h(X) = \int f_X(x) \log \frac{1}{f_X(x)} \, dx\]가 미분 엔트로피이다.
미분 엔트로피 $h(X)$는 단순히 이산화된 엔트로피 $H(X^\Delta)$와 $\log\Delta$의 차이로 같아지지 않는다.
$\Delta$가 작아질수록 $H(X^\Delta)$는 더 커지는데, 이는 $\Delta$가 작을수록 더 많은 경우의 수가 가능해져 엔트로피가 증가한다고 생각하면 된다.
이산적인 상황에서 엔트로피 $H$는 라벨 불변성(label invariance) 을 만족하지만, 미분 엔트로피는 그렇지 않다. 라벨 불변성이란, 일대일 대응 $f$에 대해 $H(X) = H(f(X))$가 성립하는 성질을 말한다.
(예시)
이산 확률변수 $X_1 \in {1,2,3}$에 대해
$P(X_1 = 1) = 0.4$, $P(X_1 = 2) = 0.5$, $P(X_1 = 3) = 0.1$라 하자. 또한 $X_2 = 2X_1 \in {2,4,6}$이며
$P(X_2 = 2) = 0.4$, $P(X_2 = 4) = 0.5$, $P(X_2 = 6) = 0.1$이다.
분포가 동일하므로 $H(X_1)$과 $H(X_2)$는 동일하다.그러나 연속 확률 변수에서는 그렇지 않다. 예를 들어 $U \sim \mathrm{Unif}(0,1)$이고 $V = 2U \sim \mathrm{Unif}(0,2)$일 때,
$h(U) = \log(1-0) = \log 1 = 0$,
$h(V) = \log(2-0) = \log 2 = 1$이다.
또한, 미분 엔트로피는 음수가 될 수도 있다. 예를 들어 $U \sim \mathrm{Unif}(0, 1/2)$라면 $h(U) = -\log 2$가 된다. 이는 미분 엔트로피가 $\log\Delta$ 항을 포함하여 정규화되기 때문이다.
2.6.4 Properties of Differential Entropy
정리 60 (상호정보량의 스케일 불변성)
정리.
\(I(aX;Y) = I(X;Y)\)
증명.
\(\begin{aligned}
I(aX;Y) &= h(aX) - h(aX \mid Y) \\
&= \big( h(X) + \log |a| \big) - \big( h(X \mid Y) + \log |a| \big) \\
&= h(X) - h(X \mid Y) \\
&= I(X;Y)
\end{aligned}\)
비고.
수식 (3)에서,
\(\begin{aligned}
h(aX \mid Y)
&= \mathbb{E} \left[ \log \frac{1}{f_{X\mid Y}(aX \mid Y)} \right] \\
&= \mathbb{E} \left[ \log \frac{1}{f_{X\mid Y}(X \mid Y)} \right] + \log |a|
\end{aligned}\)
설명.
- 이산(discrete) 변수의 경우, 1:1 변환 ( f(x) )를 해도 엔트로피는 변하지 않는다.
-
연속(continuous) 변수의 경우, 스케일 변환 ( X \to aX ) 시 차분 엔트로피는 (\log a )만큼 변한다. - 하지만 상호정보량은
( h(aX) )와 ( h(aX\mid Y) ) 모두 (\log |a|)가 더해지므로 서로 상쇄되어 변하지 않는다. - 즉, 단위 변화나 크기 스케일 변화에 대해서도 두 변수 간의 정보량은 동일하게 유지된다.
2.6.5 Joint Differential Entropy
Theorem 61 (Chain Rule of Differential Entropy).
\[h(X_1, X_2) = h(X_1) + h(X_2 \mid X_1)\]사실 discrete의 경우와 똑같다고 생각하면 된다.
Proof
$( X_1, X_2, X_3, \ldots, X_n )$ 들을 $X$ 라고 정의하자. 그러면 우리는 joint distributions에 대한 differential entropy을 정의할 수 있다.
예를 들어 $X_1$ 와 $X_2$ 가 연속적인 확률변수라면,
\[h(X_1, X_2) = \mathbb{E} \left[ \log \frac{1}{f_{X_1,X_2}(X_1,X_2)} \right]\] \[= \mathbb{E} \left[ \log \frac{1}{f_{X_1}(X_1)} \right] + \mathbb{E} \left[ \log \frac{1}{f_{X_2 \mid X_1}(X_2 \mid X_1)} \right]\] \[= h(X_1) + h(X_2 \mid X_1)\]위와 같이 나타낼 수 있다. 이는 pmf(discrete)의 성질과 동일하다. 결합 확률은 주변확률과 조건부 확률의 곱으로 나타낼 수 있는데, pdf(continuous)에서도 동일하게 성립한다.
Theorem 62.
$X$ 와 $Y$ 가 독립이라는 것은 다음과 필요충분조건이다.
Theorem 63 (Data Processing Inequality).
( X - Y - Z ) 가 Markov chain을 형성한다면
Proof
조건은 엔트로피를 감소시키지않기 때문에
첫번째 등식은 Markov property $f(Z \mid Y) = f(Z \mid Y, X)$ 에서 나온다.
2.6.6 Maximum Differential Entropy
이산 변수에서 최대 엔트로피는 균등 분포에서 달성된다.
이산 확률 변수 $X \in {1, 2, \dots, K}$의 엔트로피는 다음 부등식을 만족한다. $H(X) \leq \log_2 K$
등호는 균등 분포일 때 성립한다.
2차 모멘트 제약 조건
확률 변수 $X$가 다음을 만족한다고 가정한다.
\[\mathbb{E}[X^2] \leq P\]이 조건 하에서, 미분 엔트로피가 최대가 되는 분포는 무엇인가?
정리65. 가우시안 분포가 최대 미분 엔트로피를 가진다.
proof.
$X$의 확률 밀도 함수를 $f_X$,
평균 0, 분산 $P$인 가우시안 확률 변수 $X’ \sim \mathcal{N}(0, P)$의 pdf를
라고 하자.
KL 발산의 정의에 의해,
\[D(f \| g) = \mathbb{E}_f \left[\log \frac{f_X(X)}{g(X)}\right]\] \[D(f \| g) = \mathbb{E}_f \left[\log \frac{1}{g(X)}\right] - \mathbb{E}_f \left[\log \frac{1}{f_X(X)}\right] = \mathbb{E}_f \left[\log \frac{1}{g(X)}\right] - h(f_X)\]여기서 $h(f_X)$는 확률 변수 $X \sim f_X$의 미분 엔트로피이다.
\[\mathbb{E}_f \left[\log \frac{1}{g(X)}\right] = \log \sqrt{2 \pi P} + \frac{\mathbb{E}_f [X^2]}{2P}\]그리고 $\mathbb{E}_f[X^2] = \mathbb{E}_g[X^2] = P$이므로,
\[\mathbb{E}_f \left[\log \frac{1}{g(X)}\right] = \log \sqrt{2 \pi P} + \frac{P}{2P} = \log \sqrt{2 \pi P} + \frac{1}{2} = h(g)\] \[D(f \| g) = h(g) - h(f_X) \geq 0\]$D(f | g)$은 K-L Divergence이므로 항상 0 이상이다.
\[h(g) \geq h(f_X)\]$\therefore$ 2차 모멘트 제약 조건 하에서 가우시안 분포가 최대 미분 엔트로피를 가진다.